Algoritmi di ordinamento e ricerca
Lo scopo di questo lavoro è quello di proporre un’unità didattica sugli algoritmi di ordinamento e ricerca.
Nota: questa pagina è da considerarsi "under construction". L'indice e il contenuto stesso delle sezioni potranno subire modifiche, aggiunte e/o rimozioni nel corso delle prossime settimane. --Salvatore Parlato (discussioni) 12:34, 3 mag 2015 (CEST)
Indice |
Premessa
Partendo dalla ferma convinzione che uno degli obiettivi primari della scuola sia quello di trasmettere conoscenze a lungo termine anziché inculcare nozioni mnemoniche e ammaestrare gli studenti all’uso di particolari strumenti, ho deciso di concentrare l’attenzione sulla spiegazione degli algoritmi piuttosto che sulla loro implementazione in un particolare linguaggio di programmazione. Pertanto queste pagine presenteranno una selezione, quanto più possibile organica, di attività “unplugged” – adattate a partire da materiale già disponibile in rete o inventate all’occorrenza - che illustrano alcuni dei principali algoritmi di ordinamento e ricerca, attraverso analogie ed applicazioni degli stessi a problemi della vita “reale”. Si farà quindi largo uso di giochi, video e teatralizzazioni per condurre gli studenti a ricavare direttamente in prima persona i passi elementari degli algoritmi via via affrontati. Com’è ovvio, non mancheranno esempi di implementazione, presentati però attraverso una pseudo-codifica; tale scelta è stata effettuata sia per lasciare al docente la libertà di scegliere il linguaggio che egli ritenga più opportuno rispetto al contesto in cui si trovi ad operare, sia per contribuire a focalizzare maggiormente l’attenzione dello studente sul “cosa” l’algoritmo debba fare rispetto al “come” questo venga implementato.
L’unità didattica è pensata per essere utilizzata in una classe terza di un istituto tecnico industriale ad indirizzo informatico; non vi sono, però, controindicazioni al suo utilizzo in toto o in parte in diversi contesti scolastici (altri indirizzi di studio o anni di corso). Come prerequisiti per l’efficacia didattica sono richiesti una buona padronanza dei costrutti di selezione e iterazione, la conoscenza del concetto di variabile e di almeno una struttura dati lineare (ad esempio il vettore). E un mazzo di carte!
Ordinamento
Introduzione
La necessità di ordinare nasce da molte esigenze della vita quotidiana: fornire un elenco di nomi in ordine alfabetico, stilare la classifica di una gara… o banalmente sistemare gli oggetti in ordine in modo che sia facile ritrovarli, ad esempio...
"ORDINARE significa disporre un insieme di oggetti omogenei secondo un criterio che stabilisca la modalità di disposizione degli elementi nell’insieme stesso" (Camagni-Nikolassy, Corso di informatica 2)
Anche alcuni giochi che sicuramente conoscete, come i solitari con le carte, hanno come scopo l’ordinamento di un insieme. Il solitario, però, pur essendo composto da un insieme di regole che guidano il giocatore passo dopo passo, non è un algoritmo. Può capitare infatti che durante una partita ci si blocchi in un punto e non ci sia nessuna regola che ci consenta di andare avanti: le regole, quindi, non sono complete. Succede, inoltre, che continuiamo a scorrere il mazzo degli “scarti” senza che nessuna delle carte possa essere posizionata, finendo in un ciclo infinito (almeno finché non ci annoiamo e ricominciamo un’altra partita!): il gioco, quindi, non sempre termina e i passi non sono finiti. Inoltre, capita spesso di trovarsi di fronte a due o più possibili scelte e non c’è una regola che ci dica quale sia quella giusta e quale invece ci farà perdere la partita: le regole non sono deterministiche.
Esistono, invece, centinaia di algoritmi che risolvono il problema dell’ordinamento e i ricercatori continuano a studiarne di nuovi per migliorare e ottimizzare l’elaborazione: vedremo, infatti, che l’ordinamento è un problema piuttosto semplice finché ci si limita a insiemi di pochi elementi, ma all’aumentare del numero degli elementi da ordinare la complessità del problema (che in maniera semplificata può essere calcolata in funzione del numero di operazioni svolte) cresce più che proporzionalmente.
Bucket sort
Provate a pensare a come vengono sistemate di solito le posate in un cassetto: tipicamente questo è diviso in scomparti, ognuno contenente un tipo di posata (in uno le forchette, in uno i coltelli, in uno i cucchiai, ecc.)
Quest’idea è alla base di un metodo di ordinamento chiamato bucket sort.
ESERCIZIO 1: avete 20 carte estratte a caso da un mazzo, provate a ordinarle per seme (dall’1 al K e secondo la regola Cuori, Quadri, Fiori, Picche) utilizzando come piano d’appoggio tutta la cattedra. Potete utilizzare tutti gli strumenti che credete possano aiutarvi (carta, penne, pennarelli, nastro adesivo, ecc.). L’unica regola è che potete prendere le carte dal mazzo una per volta e ogni volta dovrete poggiare la carta pescata sul tavolo e non potrete più spostarla se non alla fine, quando tutte dovranno essere in ordine.
Nota: l’insegnante lascerà che gli studenti tentino di risolvere il problema applicando l’algoritmo bucket sort, stimolandoli e guidandoli nella ricerca della soluzione. Una soluzione possibile è quella di suddividere lo spazio a disposizione in quattro file (una per ogni seme); su ciascuna fila, con cartoncini e pennarelli, creare dei segnaposto per le carte ordinandoli dall’1 al K; a quel punto ogni volta che viene estratta una carta dal mazzo non resta che sistemarla in corrispondenza del segnaposto corretto. Alla fine basterà ricomporre il mazzo raccogliendo le carte una fila alla volta.
Scriviamo l’algoritmo:
Ripeti per quanti elementi ci sono nell’insieme da ordinare
Estrai un elemento
Sistemalo nel posto corretto nello spazio di appoggio
Ripeti per quanti elementi ci sono nell’insieme da ordinare
Raccogli gli elementi uno per uno nell’ordine in cui sono sistemati nello spazio di appoggio
Come avrete notato è un sistema piuttosto veloce per ordinare, poiché avete dovuto scorrere il mazzo una sola volta e ogni volta siete riusciti a sistemare la carta nella posizione corretta. Il problema è che richiede molto spazio: supponiamo infatti che non abbiate un piano di appoggio, dovremo trovare qualche altro algoritmo che ci aiuti a risolvere il problema.
Selection sort
ESERCIZIO 2: avete 20 carte estratte a caso da un mazzo. Divisi in coppie, provate ad ordinare le carte dalla più piccola alla più grande (a parità di valore si rispetta l’ordine cuori, quadri, fiori, picche). Le regole questa volta sono: potete scorrere il mazzo quante volte volete, ma sempre girando una carta per volta. Potete chiedere al vostro compagno di tenere in mano una carta per voi, ma solo una carta per volta. Potete impilare sul banco il mazzo ordinato via via che questo viene a formarsi.
Nota: l’insegnante lascerà che gli studenti tentino di risolvere il problema applicando l’algoritmo selection sort, stimolandoli e guidandoli nella ricerca della soluzione. Un possibile aiuto da dare agli studenti è aggiungere la regola per cui, ogni volta che si è completata una scansione del mazzo, solo la carta in mano al compagno “di appoggio” potrà essere sistemata sul tavolo a riformare il mazzo ordinato.
Bene! Abbiamo risolto il problema dello spazio… purtroppo però vi sarete accorti che ci è voluto molto più tempo. Quante volte avete dovuto scorrere il mazzo? Provate a estrarre altre 20 carte e ripetere l’esercizio contando quante volte scorrete il mazzo prima di completare l’ordinamento.
Avrete notato che, indipendentemente da quali carte vengono estratte, bisogna scorrere il mazzo sempre lo stesso numero di volte. Qual è questo numero? Esatto, il numero delle carte meno una!
Scriviamo l’algoritmo:
Ripeti per quanti sono gli elementi dell'insieme da ordinare meno uno
Ripeti per quanti sono gli elementi ancora da ordinare
Estrai un elemento
Se l'elemento esaminato vale meno di quello nello spazio di appoggio
Sostituisci l'elemento nello spazio di appoggio con quello corrente
Vai all'elemento successivo
L'elemento rimasto nello spazio d'appoggio è il prossimo nell'ordine corretto
L'elemento rimasto è l'ultimo dell'insieme ordinato
Questo algoritmo prende il nome di Selection Sort, poiché ad ogni iterazione viene selezionata la cara che occuperà la posizione successiva nel mazzo secondo il criterio d’ordine che si è scelto.
ESERCIZIO 3: scrivere un programma che riempia un vettore di dimensione casuale N (compresa tra 10 e 50) con numeri estratti a caso tra 1 e 200 e lo ordini secondo l'algoritmo Selection Sort. Il programma deve dare in output: il vettore generato casualmente, il vettore ordinato, il numero di volte in cui l'algoritmo esegue una scansione completa del vettore.
Nota: far riflettere gli studenti sul fatto che, detto N il numero delle carte estratte, le volte che bisogna scorrere il mazzo per terminare l’algoritmo sono sempre N-1 e non N perché è impossibile che le carte siano tutte in ordine tranne una
L’algoritmo ha anche un’altra caratteristica: provate a contare, per ogni volta che scorrete completamente le carte che avete ancora in mano, quanti confronti eseguite. Cosa si può notare?
ESERCIZIO 4: aggiungere all'output del programma dell'esercizio 3 il numero di confronti effettuati dall'algoritmo per ogni scansione completa del vettore.
Nota: far riflettere gli studenti sul fatto che, ad ogni iterazione, il numero di confronti diminuisce di uno. Il totale dei confronti è quindi dato da (N-1)+(N-2)+…+1, cioè N(N-1)/2 ed è indipendente da quali carte vengono estratte e dal loro ordine iniziale.
Come detto questo algoritmo, per quanto semplice, è purtroppo lento. Abbiamo infatti notato che il numero di confronti che dobbiamo fare non dipende da quali carte dobbiamo ordinare, né dall’ordine in cui ci si presentano ma solo dal loro numero: possiamo quindi dire che la complessità dell’algoritmo non dipende dalle caratteristiche dei dati in ingresso ma solo dalla dimensione dell’insieme da ordinare. Gli algoritmi con questa caratteristica si dicono non adattivi. Possiamo inoltre notare che, anche se le carte che ci rimangono in mano sono già nell’ordine corretto, l’algoritmo ci impone di continuare a eseguire tutti i confronti rimanenti.
Bubble sort
Osserviamo adesso questo video e proviamo a capire se ci suggerisce un metodo per risolvere il prossimo esercizio.
ESERCIZIO 5: avete 20 carte estratte a caso da un mazzo. Provate a ordinarle dalla più piccola alla più grande (a parità di valore si rispetta l’ordine cuori, quadri, fiori, picche) usando solo le vostre mani. Non potrete appoggiare le carte né utilizzare un compagno che vi aiuti. Potete, come prima, esaminare le carte e confrontarle al massimo due per volta.
Nota: l’insegnante lascerà che gli studenti tentino di risolvere il problema applicando l’algoritmo bubble sort, stimolandoli e guidandoli nella ricerca della soluzione. Un possibile aiuto da dare è suggerire agli studenti di esaminare ed eventualmente scambiare solo carte consecutive.
Avrete notato una differenza importante rispetto all’esercizio precedente: quando ci si accorge che non si effettuano più scambi si è certi che le carte sono già ordinate ed è possibile fermarsi. Si nota inoltre che, per ogni scansione del mazzo, il numero di confronti è N-1 (dove N è la dimensione del mazzo stesso).
Scriviamo l’algoritmo:
Ripeti finché fai almeno uno scambio
Ripeti per quanti sono gli elementi da ordinare meno uno
Estrai un elemento
Se l'elemento esaminato è maggiore di quello che lo segue nell'insieme
Scambiali
Vai all'elemento successivo
Questo metodo ha, però, un’altra caratteristica: dopo la prima scansione del mazzo la carta più alta raggiunge la sua posizione finale in coda al mazzo, dopo la seconda scansione la seconda carta più alta viene a trovarsi nella posizione corretta, cioè la penultima, e così via… dopo ogni scansione del mazzo via via la carta più alta tra quelle rimaste da ordinare si sposta verso la sua posizione corretta in coda al mazzo, proprio come le bollicine in un bicchiere di spumante tendono a risalire verso l’alto: per questo motivo l’algoritmo che abbiamo appena visto è chiamato Bubble Sort.
Questa caratteristica ci suggerisce una possibile ottimizzazione dell’algoritmo: se nella prima scansione dobbiamo confrontare tra loro tutte le N carte che abbiamo in mano, nella seconda sappiamo già che la carta più grande è correttamente posizionata in coda al mazzo, quindi restano da confrontare N-1 carte; nella terza scansione le carte da confrontare saranno N-2 e così via. Non solo, se guardiamo di nuovo il video dei ballerini, ci accorgiamo che, in realtà, dopo ogni scansione i numeri ancora da ordinare si trovano tutti a sinistra della posizione in cui è avvenuto l’ultimo scambio, la stessa cosa succede col vostro mazzo di carte: questo ci suggerisce che, per ottimizzare ulteriormente l’algoritmo, ad ogni iterazione possiamo arrestare la scansione del mazzo alla posizione in cui è avvenuto l’ultimo scambio dell’iterazione precedente. Quindi, una possibile versione ottimizzata dell’algoritmo è:
Ripeti finché fai almeno uno scambio
Ripeti per quanti sono gli elementi da ordinare meno quelli che seguono la posizione dell’ultimo scambio
Estrai un elemento
Se l'elemento esaminato è maggiore di quello che lo segue nell'insieme
Scambiali
Vai all'elemento successivo
ESERCIZIO 6: scrivere un programma che riempia un vettore di dimensione casuale N (compresa tra 10 e 50) con numeri estratti a caso tra 1 e 200 e lo ordini secondo l'algoritmo Bubble Sort. Il programma deve dare in output: il vettore generato casualmente, il vettore ordinato, il numero di confronti eseguiti.
Se proviamo a contare il numero di confronti effettuati, ci accorgiamo che, a differenza del Selection Sort, questo cambia a seconda dall’ordine in cui si presentano le carte estratte. Nel caso in cui le carte siano già ordinate, infatti, l'algoritmo esegue soltanto una scansione del mazzo (N-1 confronti) e termina. Nel caso peggiore, invece, in cui le carte sono esattamente nell’ordine inverso rispetto a quello che vogliamo, il numero di confronti è N(N-1)/2, lo stesso del Selection Sort.
Algoritmi "lenti" e "veloci"
Ecco quindi che cominciamo a renderci conto di come il problema dell’ordinamento, al crescere del numero N di elementi da ordinare, possa diventare estremamente complesso: sia il selection sort che il bubble sort, infatti, eseguono un numero di confronti che, al crescere di N, è proporzionale ad N2
Supponiamo allora che il nostro computer sia in grado di eseguire un’operazione di confronto in un microsecondo (cioè la milionesima parte di un secondo) e proviamo a calcolare il tempo che impiegherebbe ad ordinare un insieme di N elementi al crescere di N usando uno di questi algoritmi.
| N=10 | N=100 | N=1.000 | N=10.000 | N=1.000.000 |
|---|---|---|---|---|
| ~0,0001 s | ~0,01 s | ~1 s | ~100 s | ~1.000.000 s (~12 giorni) |
Quindi per ordinare l’Oxford English Dictionary, uno dei dizionari più grandi del mondo, contenente circa 500.000 lemmi, eseguendo sulla macchina che abbiamo considerato uno di questi algoritmi, ci potrebbe volere qualche giorno (pensate che la sua prima edizione è stata pubblicata nel 1928 e per la sua compilazione sono stati necessari circa 70 anni... ah se avessero avuto a disposizione un computer!).
Ma allora non c’è un modo per andare più veloce? Cominciamo con un filmato... attenzione a cosa fa la bambina!
Allora? Cosa avete notato? Il bambino ha ordinato i contenitori usando un algoritmo che già conoscete, chi l’ha riconosciuto? Esatto, era il Selection Sort! Il bambino ha confrontato ogni contenitore con tutti gli altri per individuare di volta in volta il più pesante tra quelli rimasti. La bambina, invece, ha utilizzato un approccio diverso: piuttosto che confrontare ogni contenitore con tutti gli altri, ogni volta ha diviso l’insieme dei contenitori da ordinare in due gruppi, dopodiché ha ri-applicato lo stesso procedimento ai gruppi più piccoli, e così via finché il problema non si è ridotto a confrontare delle coppie. Ha cioè provato a dividere il problema in problemi più semplici: questa tecnica, in informatica, si chiama Divide et impera (che in latino significa separa e comanda) e pare si ispiri niente meno che a Filippo II di Macedonia, grande re dell’antichità che, per mantenere il potere, adottò la strategia di separare e mettere in lotta fra loro i suoi oppositori per evitare che si unissero contro di lui.
Questa strategia funziona molto bene con i problemi di ordinamento (la bambina infatti ha terminato molto prima del suo amico): il motivo è che, come abbiamo già detto, la complessità dei problemi di ordinamento aumenta all'aumentare del numero di elementi nell'insieme da ordinare, cioè all'aumentare della sua cardinalità. Quindi più è piccolo l'insieme da ordinare più sarà semplice ordinarlo, il caso più semplice è quello in cui bisogna confrontare due soli elementi: questa è proprio la considerazione su cui si basa la strategia Divide et impera! L'insieme da ordinare (il problema) viene suddiviso secondo un certo criterio in insiemi più piccoli (sotto-problemi) e il procedimento viene ripetuto finchè la dimensione dei sotto-problemi non raggiunge quella del problema elementare (nel nostro caso confrontare due elementi e decidere qual è più grande). Alla fine basterà combinare le soluzioni di tutti i sotto-problemi (le coppie ordinate) per ottenere la soluzione del problema iniziale (l'insieme ordinato).
Merge sort
Ora che conoscete la strategia Divide et impera provate ad individuare come viene applicata in questo video e utilizzatela per ordinare il nostro solito mazzo di carte!
ESERCIZIO 7: avete 20 carte estratte a caso da un mazzo, provate ad ordinare le carte dalla più piccola alla più grande (a parità di valore si rispetta l’ordine cuori, quadri, fiori, picche). Le regole questa volta sono: potete usare soltanto le vostre mani; ognuno di voi può scambiare tra loro soltanto due carte tra quelle in suo possesso; potete chiedere a un compagno di prendere un certo numero delle vostre carte e restituirvele ordinate (ovviamente anche il compagno dovrà rispettare le stesse regole).
Nota: l’insegnante lascerà che gli studenti tentino di risolvere il problema applicando l’algoritmo merge sort, stimolandoli e guidandoli nella ricerca della soluzione. Un possibile suggerimento da dare agli studenti è quello di cedere ad un compagno metà delle proprie carte finchè non ne restano in mano soltanto due.
Ottimo! L'algoritmo che avete utilizzato si chiama Merge Sort: l'idea, infatti, è quella di continuare a dividere a metà l'insieme da ordinare in insiemi sempre più piccoli fino ad ottenere delle coppie. Poi, una volta ordinate le coppie, "fonderle" a due a due per ottenere insiemi ordinati di quattro elementi, poi di otto e così via via fino a ricostruire l'insieme iniziale ordinato.
Proviamo a scrivere l'algoritmo
Se hai più di un elemento
Dividi l'insieme a metà
Richiama l'algoritmo mergesort sulla prima metà
Richiama l'algoritmo mergesort sulla seconda metà
Richiama la funzione di fusione delle due metà
La funzione di fusione preleva l'elemento più piccolo fra quelli che si trovano in cima alle due metà e questo diventa il primo del nuovo insieme. Il procedimento è ripetuto finché non si esauriscono gli elementi di una delle due metà, a quel punto quelli rimanenti sono già ordinati e vengono accodati al nuovo insieme.
Ecco un'ulteriore immagine di esempio...
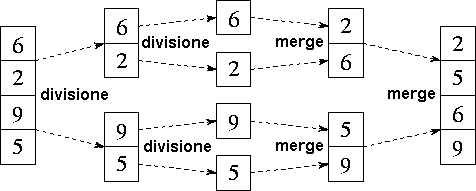
...e un altro video che spiega l'algoritmo soffermandosi sul concetto di "fusione" di due insiemi ordinati.
Nota: il video è in inglese e i sottotitoli sono fatti evidentemente con un traduttore automatico, sembra comunque abbastanza chiaro per essere proposto ugualmente a studenti di scuola superiore, in alternativa è comunque possibile realizzare direttamente in classe l'attività "unplugged" proposta per spiegare il concetto di "merge".
Come avrete notato l'algoritmo ha la caratteristica di richiamare ripetutamente se stesso: gli algoritmi di questo tipo si dicono ricorsivi.
ESERCIZIO 8: scrivere un programma che riempia un vettore di dimensione casuale N (compresa tra 10 e 50) con numeri estratti a caso tra 1 e 200 e lo ordini secondo l'algoritmo Merge Sort. Il programma deve dare in output: il vettore generato casualmente, i sotto-vettori che di volta in volta vengono passati al metodo per ogni sua chiamata ricorsiva, i sotto-vettori ordinati, il vettore iniziale ordinato.
Proviamo ora a stimare la complessita di questo algoritmo.
ESERCIZIO 9: aggiungere all'output dell'esercizio precedente l'indicazione del numero di chiamate ricorsive effettuate e, per ognuna, il numero di confronti effettuati dalla funzione di fusione dei sott-vettori.
Possiamo notare che il numero di chiamate ricorsive effettuate dipende dalla dimensione del vettore da ordinare. Questo, infatti, viene sempre diviso in due parti uguali finchè queste non raggiungono la dimensione del caso base (1 o 2 elementi): il numero di chiamate ricorsive (la profondità) sarà, quindi, sempre log2(N). Inoltre, per fondere due insiemi di N/2 elementi servono al più N confronti: moltiplicando quindi il numero di chiamate ricorsive per il numero massimo di confronti effettuati ad ogni chiamata otteniamo che, anche nel caso peggiore, il Merge Sort esegue un numero di confronti proporzionale a N*log2(N).
ESERCIZIO 10: scrivere un programma che generi 100 vettori di dimensione casuale tra 10 e 100 con numeri casuali compresi tra 1 e 200 e li ordini usando per ognuno tutti e tre gli algoritmi visti finora. Il programma deve dare in output il numero di confronti effettuati da ciascun algoritmo per ordinare ciascun vettore. Utilizzando i dati forniti dal programma costruire un grafico che abbia in ascissa la dimensione N del vettore e in ordinata il numero di confronti effettuati per ordinarlo.
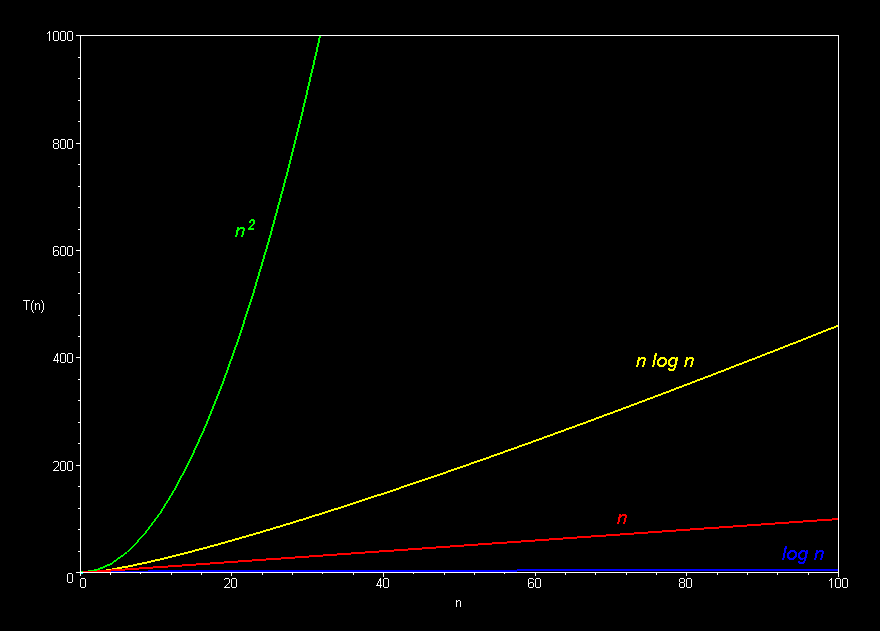
Siete risuciti a risolvere l'esercizio? Bene, allora avrete ottenuto un grafico simile a quello riportato di seguito. La curva verde rappresenta una complessità proporzionale ad N2 e come detto è propria degli algoritmi che abbiamo definito "lenti", ad esempio Selection Sort e Bubble Sort: come vedete la curva è molto "ripida" cioè il numero di confronti necessario a completare l'algoritmo cresce molto rapidamente all'aumentare della dimensione del problema. La complessità del Merge Sort (N*log2N) è invece rappresentata dalla curva gialla: questa ha una pendenza molto più "dolce", il numero di confronti necessario, infatti, cresce molto meno rapidamente all'aumentare della cardinalità dell'insieme di dati da ordinare, l'algoritmo è più "veloce".
Il Merge Sort ha, però, un difetto: se ricordate, quando l'avete applicato al mazzo di carte avete dovuto ricorrere all'aiuto dei compagni. L'algoritmo, infatti, non può essere eseguito in place (sul posto), c'è bisongo di allocare ulteriore spazio dove "appoggiare" temporaneamente i dati durante la sua esecuzione. Proviamo allora a trovare un altro metodo "veloce", che utilizza la tecnica del divide et impera, ma che sia anche eseguibile in place.
Quick sort
Proviamo a guardare questo video.
L'algoritmo illustrato si chiama Quick Sort. L'idea di base è, come nel Merge Sort, quella di dividere il problema in problemi più piccoli fino a che non si raggiunge il caso base: è, dunque, un altro algoritmo che usa la tecnica del divide et impera; in questo caso, però, l'insieme di dati da ordinare viene diviso in due parti prendendo come riferimento un elemento dell'insieme stesso (chiamato pivot) e separando gli altri ponendo da una parte tutti gli elementi più piccoli del pivot e dall'altra tutti quelli più grandi. L'algoritmo poi procede ricorsivamente applicando lo stesso procedimento ai due sottoinsiemi appena generati... e così via finchè gli insiemi non sono composti da due soli elementi che possono banalmente essere ordinati per confronto diretto.
ESERCIZIO 11: avete 20 carte estratte a caso da un mazzo, provate ad ordinare le carte dalla più piccola alla più grande (a parità di valore si rispetta l’ordine cuori, quadri, fiori, picche) utilizzando l'algoritmo Quick Sort.
Proviamo a scrivere l'algoritmo
Se hai più di un elemento
Scegli un elemento pivot
Ripeti per quanti sono gli elementi da ordinare
Se un elemento è più piccolo del pivot
Spostalo a sinistra del pivot
Se un elemento è più grande del pivot
Spostalo a destra del pivot
Richiama l'algoritmo quicksort sugli elementi a sinistra del pivot
Richiama l'algoritmo quicksort sugli elementi a destra del pivot
Questo video spiega di nuovo l'algoritmo che avete appena imparato suggerendo come implementare con due indici le operazioni di selezione del pivot e partizionamento degli elementi rimanenti a destra e sinistra del pivot.
A differenza del Merge Sort, quindi, il Quick Sort è realizzabile in place. Purtroppo, però, avrete notato che non sempre l'insieme da ordinare viene diviso in due parti esattamente uguali tra loro. Questo significa che il numero di chiamate ricorsive è log2N solo nel caso migliore mentre può diventare N-1 nel caso peggiore... che è per assurdo quello dell'insieme già ordinato! (o ordinato al contrario). Il numero di confronti necessari ad ogni chiamata ricorsiva dell'algoritmo è N-1. La complessità quindi dipende da come si presentano i dati in ingresso e da come viene scelto di volta in volta l'elemento pivot: è proporzionale a N*log2N nel caso medio ma può diventa proporzionale a N2 nel caso peggiore.
Questo video confronta difetti e benefici dei due algoritmi "veloci" che abbiamo appena visto.
Ricerca
Introduzione
Cercare un elemento in un insieme è un problema che affrontiamo quasi quotidianamente: pensate ad esempio a quando cercate il numero di un vostro amico nella rubrica del vostro telefonino o quando a casa cercate il cd che volete ascoltare nel mucchio (non sempre ordinato) di tutti i vostri dischi. Il problema, come avrete potuto sperimentare più volte, non è sempre di facile soluzione… soprattutto se non si usa il metodo adatto! Esempio.
Per fortuna anche in questo caso, come per il problema dell'ordinamento, esistono diversi algoritmi che possiamo usare: l'importante è come al solito scegliere quello giusto! Ecco un esempio di alcuni algoritmi di ricerca all'opera su un problema.
Ricerca Lineare
ESERCIZIO 1: ciascuno di voi peschi una carta a caso da un mazzo; uno di voi ha il compito di scoprire quale compagno ha l’asso di picche. La regola è che potrà chiedere ai compagni di mostrargli la propria carta, ma solo una per volta. Esempio di svolgimento dell'attività
E’ banale intuire che l’unico modo per trovare un elemento in un insieme non ordinato è quello di controllare uno per volta gli elementi dell’insieme finché non si trova l’elemento cercato. Questo metodo di ricerca è un algoritmo e prende il nome di Ricerca Lineare. Se riflettete è lo stesso metodo che usate inconsciamente in tantissime occasioni: per cercare un cd nella pila di dischi che avete a casa o per trovare il libro che vi serve nello zaino; ogni volta che bisogna trovare qualcosa in un insieme che non sia ordinato ci affidiamo alla ricerca lineare.
Scriviamo l’algoritmo
Posizionati sul primo elemento dell’insieme
Ripeti finché non trovi l’elemento cercato e ci sono ancora elementi nell’insieme
Se l’elemento corrente è quello cercato
TROVATO!
Altrimenti
Vai all’elemento successivo
Potete usare questo algoritmo anche come strategia per giocare al gioco dell’impiccato. Il vostro obiettivo, infatti, è trovare tra le lettere dell’alfabeto quelle che sono presenti nella parola da indovinare. Un metodo possibile è quello di provare con le lettere in ordine alfabetico… ma forse ce n’è uno che funziona meglio, pensateci!
Nota: una strategia migliore è scegliere le lettere secondo la loro frequenza d’uso nella lingua in cui si sta giocando. In italiano, ad esempio, le lettere E, A, I, O, N, L sono le più usate e sarà più facile trovarne una rispetto a lettere come B, Q, Z.
Lo stesso metodo è stato usato da Jean-Dominique Bauby per dettare il suo libro "Lo scafandro e la farfalla". Il giornalista francese, infatti, era purtroppo rimasto completamente paralizzato in conseguenza di un ictus; l’unico movimento controllato di cui aveva facoltà era quello di una palpebra. Il libro, autobiografico, parla proprio della sua sindrome locked-in ed è stato scritto utilizzando, appunto, l’algoritmo di ricerca lineare. L’assistente di Bauby gli recitava le lettere dell’alfabeto secondo la frequenza d’uso nella lingua francese (E, S, A, R, I, N, T, U, L, O, M, P, D, C, F, B, V, H, G, J, Q, Z, Y, K, X, W) e l’autore sbatteva la palpebra quando il suo assistente pronunciava la lettera corretta. Per comporre una parola occorrevano circa 2 minuti e per scrivere l’intero libro sono stati necessari circa 200.000 battiti di palpebra.
Proviamo a studiare la complessità di questo algoritmo. Se siamo fortunati l’elemento che stiamo cercando è proprio il primo dell’insieme per cui basta un solo confronto per terminare la ricerca. Purtroppo pero, se l’elemento cercato non è tra quelli presenti nell’insieme possiamo accorgercene solo dopo averli controllati tutti: in questo caso, quindi, sono necessari N confronti (detta N la cardinalità dell’insieme). E nel caso medio?
ESERCIZIO 2: scrivere un programma che generi un vettore di dimensione 50 riempiendolo casualmente con tutti i numeri compresi tra 1 e 50. Il programma ripete 1000 volte la ricerca di un numero a caso tra 1 e 50 e restituisce la media dei confronti effettuati. Ripetere il calcolo cercando un numero compreso tra 1 e 100. Confrontare i risultati.
ESERCIZIO 3: modificare il programma per studiare la variazione del numero di confronti necessari a completare la ricerca al variare della dimensione del vettore tra 10 e 1000.
L’algoritmo di ricerca lineare effettua mediamente N/2 confronti per trovare l’elemento cercato. Si dice che questo algoritmo ha complessità lineare.
Come detto questo algoritmo si applica ad insiemi di dati non ordinati, inoltre ci sono strutture dati per cui questo è l’unico algoritmo di ricerca possibile. Pensate alle vecchie musicassette: l’unico modo per ascoltare la canzone scelta era scorrere tutto il nastro fino a posizionarci in corrispondenza dell’inizio della canzone. Anche in informatica esistono strutture dati di questo tipo, in cui l’accesso ai dati avviene soltanto in maniera sequenziale, cioè partendo dal primo elemento dell’insieme e scorrendoli tutti fino a quello desiderato; in strutture dati di questo tipo l’unico algoritmo di ricerca applicabile è, appunto, quello lineare.
Ricerca Binaria
Chi di voi ha mai giocato a Indovina Chi?
Per chi non lo conoscesse, è un gioco (molto popolare negli anni '90) in cui bisogna indovinare quale personaggio misterioso ha estratto l'avversario in un insieme di 24 personaggi possibili, ponendogli delle domande sulle caratteristiche fisiche del personaggio misterioso. Si tratta quindi, anche in questo caso, di un problema di ricerca; l'algoritmo di rierca lineare, però, non è il modo più furbo per costruire una strategia vincente: eliminando un personaggio per volta, infatti, occorrerebbero in media 12 turni per arrivare alla soluzione. Qual è allora una strategia migliore? Esatto, porre domande che ci consentano di eliminare più personaggi alla volta! Ma allora, quali sono le migliori domande da porre? Provate ad osservare questo video e vediamo un po' se vi suggerisce qualche idea.
Sì, si tratta di nuovo di applicare la strategia divide et impera! Le domande migliori sono quelle che ogni volta ci consentono di eliminare metà delle opzioni possibili: supponendo, infatti, di riuscire a dividere sempre per 2 le opzioni rimaste, siamo sicuri di arrivare a dare la risposta in al più 6 turni (metà di quanti ne occorrerebbero in media con una ricerca lineare!).
Questo algoritmo prende il nome di Ricerca Binaria o Dicotomica dal greco διχοτομία , dichotomìa: composto da δίχα (dìcha, in due parti) e τέμνω (témno, divido) che significa proprio dividere in due parti.
ESERCIZIO 4: provate a cercare, in un mazzo di carte, il 7 di cuori, usando l'algoritmo di ricerca binaria.
Come avrete notato questo algoritmo ha una caratteristica: funziona solo se l'insieme dei dati su cui viene applicato è ordinato!
Proviamo a scrivere l'algoritmo, usando come al solito una pseudo-codifica
Se ci sono elementi nell'insieme
Confrontare l'elemento centrale dell'insieme con quello cercato
Se l'elemento centrale dell'insieme è quello cercato
TROVATO!
Altrimenti se l'elemento cercato è minore
Richiamare l'algoritmo sull'insieme degli elementi precedenti a quello esaminato
Altrimenti se l'elemento cercato è maggiore
Richiamare l'algoritmo sull'insieme degli elementi successivi a quello esaminato
Se ci pensate è lo stesso algoritmo che usate inconsciamente quando cercate un lemma nel vocabolario o il numero di qualcuno nell'elenco telefonico. Non potete però utilizzarlo, ad esempio, per cercare un argomento nell'indice del libro di informatica, perchè questo è ordinato per numero di pagina e non per argomento. Lo stesso Bauby avrebbe potuto utilizzare questo algoritmo per velocizzare la scrittura del suo libro se il suo assistente, invece di recitare le lettere in ordine, fosse partito dal centro e Bauby avesse risposto, ad esempio, con una strizzata d'occhio se la lettera cercata era precedente e due se era successiva.
Ragioniamo un po' sulla complessità di questo algoritmo: nel caso migliore, come per la ricerca lineare, l'elemento cercato viene trovato in un solo passo. Nel caso peggiore, però, dividendo sempre per due la sequenza di dati di cardinalità N, troveremo l'elemento cercato (o ci accorgeremo che non esiste) in al più log2N passi (approssimato per eccesso). Questo significa che per trovare un elemento tra 1.000.000 basterebbero, al più, 20 confronti.
ESERCIZIO 5: ripetere gli esercizi 2 e 3 in modo da confrontare le prestazioni dei due algoritmi di ricerca.
Bisogna osservare che la ricerca binaria è possibile soltanto su strutture dati che consentono l'accesso diretto ai dati (come ad esempio il vettore). Inoltre, come detto, il difetto di questo algoritmo è che può essere applicato solo su insiemi di dati ordinati: questo significa che al costo della ricerca va sommato quello per tenere ordinato l'insieme dei dati, costo che, come abbiamo visto, cresce rapidamente all'aumentare della cardinalità dei dati.
Cenni ad altri algoritmi di ricerca
Esistono altri algoritmi che, rilassando in qualche modo il requisito di dover operare su insiemi di dati strettamente ordinati o operando su particolari strutture dati, riescono comunque ad avere prestazioni migliori di una ricerca lineare. Vediamone qualcuno.
Radix search
Un modo efficiente di disporre i dati per velocizzare la ricerca è quello di dividerli in classi. Pensate alle rubriche telefoniche: tutti i nomi che cominciano con la stessa lettera sono scritti sulla stessa pagina della rubrica. A quel punto quando cercherete il numero di una persona il cui nome inizia, ad esempio, con la lettera R andrete direttamente alla pagnia della "R" escludendo in un sol colpo tutti i rimanenti nomi presenti nella rubrica. Questo sistema non è ottimale (lo sarebbe se tutte le pagine contenessero lo stesso numero di nomi) ma è sicuramente più veloce che fare una scansione lineare di tutti i nomi presenti nella rubrica a partire dalla prima pagina.
Il metodo può essere migliorato suddividendo a loro volta i nomi in funzione della seconda lettera.
ATTIVITA': procuratevi dei cartoncini e su ciascuno dei lati lunghi praticate 26 buchi, che contrassegnerete con le lettere dell'alfabeto (da un lato maiuscole e dall'altro minuscole). Scrivete su ogni cartoncino il nome e il numero di telefono di uno dei vostri compagni di classe, avendo cura, ogni volta che scrivete un nome, di fare un taglio sul bordo del cartoncino all'altezza del buco corrispondente alla prima lettera (lato delle maiuscole) e alla seconda lettera (lato delle minuscole) del nome del vostro compagno. Avrete in questo modo costruito una rubrica "artigianale". Se dovete cercare il numero di un vostro compagno di nome Roberto vi basterà infilare tutti i cartoncini con due spiedini di legno, uno passerà attraverso i buchi contrassegnati dalla "R" e uno attraverso quelli contrassegnati dalla "o". Agitando i due spiedini vedrete cadere sul pavimento i cartoncini contenenti i numeri di vostri compagni il cui nome comincia con "Ro" e sarà facile trovare poi tra quelli il numero giusto.
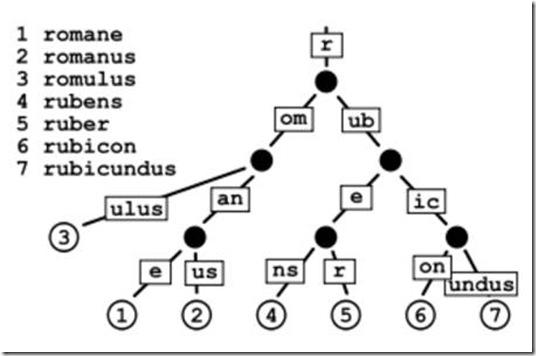
Una struttura dati che si presta particolarmente bene a questo tipo di ricerca è l'albero. Ogni nodo dell'albero rappresenta la radice di una parola, tutti i figli di quel nodo sono parole con la stessa radice. In questo caso la complessità della ricerca è proporzionale alla profondità dell'albero.
Un sistema simile è usato, ad esempio, dai sistemi di completamento automatico presenti nei vostri smartphone: il sistema vi suggerisce (tipicamente in ordine di frequenza d'uso) le parole che hanno in comune la radice che avete appena iniziato a digitare.
Hash
Ricordate l'algoritmo Bucket Sort? Anche quello si basava sulla divisione in classi dei dati da ordinare. Allo stesso modo è possibile implementare una sorta di Bucket Search; in sostanza si tratta dell'algoritmo che usate tutte le mattine quando vi vestite: se avete bisogno dei calzini sapete che dovrete cercarli nel cassetto dei calzini, le maglie probabilmente saranno nel loro cassetto e così via...
Il problema, quando si applica questo algoritmo ad insiemi di dati, è avere un metodo che ci consenta di individuare rapidamente il "cassetto" giusto, diversamente state soltanto spostando il problema dalla ricerca dell'elemento alla ricerca del cassetto. Fortunatamente questo sistema esiste e si chiama Hash. (Che curiosamente in inglese significa pasticcio, miscuglio... come potrà mai un pasticcio rendere veloce una ricerca?!)
Una funzione Hash è in grado di associare (attraverso dei calcoli) ogni elemento (e quindi la chiave di ricerca) ad uno dei contenitori. Detta N la cardinalità dei dati ed M il numero di contenitori, una buona funzione hash è in grado di suddividere in maniera uniforme i dati nei contenitori in modo che ciascuno contenga una frazione N/M di tutti i dati. Nel caso migliore in cui il numero degli elementi è uguale al numero dei contenitori il singolo elemento sarà trovato in un unico passo.
Nel caso della nostra rubrica una semplice funzione hash potrebbe associare, ad esempio, ad ogni nome il numero dato dalla somma delle cifre corrispondenti alla posizione nell'alfabeto delle prime due lettere da cui è composto; quel numero sarà poi il numero della pagina della rubrica in cui nome e numero saranno annotati.
ATTIVITA': provate a realizzare una rubrica con i numeri di telefono dei vostri compagni utilizzando la funzione hash suggerita o inventandone una a vostro piacimento.
Avrete notato che usando una funzione hash può capitare che due persone che abbiano i nomi che cominciano in maniera diversa possano andare a finire sulla stessa pagina; non solo, è anche possibile che ci siano parecchie pagine che non contengono nessun nome.
L'hash è un compromesso tra tempo necessario alla ricerca e spazio sprecato per salvare i dati: da un lato abbiamo, come detto, un elemento in ogni "contenitore" che ci consente di trovare ciascun elemento con complessità 1 al prezzo di avere almeno tanti contenitori quanti sono gli elementi dell'insieme; dall'altro lato se avessimo un solo contenitore per tutti gli elementi avremmo sicuramente molto meno spazio sprecato al prezzo però di una ricerca molto più lenta.
Tutti voi (beh forse tutti) avete assistito, senza saperlo, ad un hashing
Sì, proprio il cappello parlante di Harry Potter (in inglese guardacaso si chiama Sorting Hat) che "magicamente" (o attraverso calcoli, chi può dirlo?!) divide i nuovi studenti (dati) nelle relative case (contenitori). Per essere una vera e propria funzione hash dovrebbe anche essere in grado di rispondere alla domanda "Di quale casa fa parte lo studente X?"... purtroppo nei libri nessuno gliel'ha mai posta e non lo sapremo mai.
Riferimenti
L'esempio del solitario e alcune delle attività proposte si ispirano al libro di Paul Curzon Computing Without Computers
Il video del confronto tra algoritmi di ricerca è tratto da Computer Science Unplugged
L'immagine del cassetto delle posate è presa dal sito ordinata-mente
L'immagine di esempio del Merge Sort è presa dal sito dell'IIS Marconi di Latina
Il grafico sulla complessità degli algoritmi è preso dal sito del Prof. Jim Marshall
L'immagine del radix tree è tratta da wikipedia
L'immagine del cappello parlante è presa da questo wiki
Altre fonti: